√ ベクトル 平行 条件 149187-ベクトル 平行 条件

図を描いてベクトルの向きに気をつけるようにしましょう。 また，向かい合う辺をベクトルで考えればよいので四角形 A B C D が平行四辺形である条件は A D → = B C → などでもかまいません。さらに，ベクトル同士の和やk 倍は，成分ごとの和やk 倍になり，数ベクト ルとしての和やk 倍と一致する．すなわち，幾何ベクトルが数ベクトルで表 される． 共線条件 相異なる2点A,B を考え，位置ベクトルをa, b とする．点P（位置ベ共線条件とは、三点が一直線上に存在するときに成立する条件の事で、 例えば点bが直線ac上にある時、 ab=kac (kは実数) の様に始点(ここではa)を揃えると、 abベクトルはacベクトルのk倍という式が成立します。これがベクトルでの共線条件です。

基本 空間ベクトルの成分と平行 数ｂ空間ベクトル2 09 Youtube

ベクトル 平行 条件

ベクトル 平行 条件-に分けると， ということは， この2つのベクトルの平行条件そのものです． これはどういうことでしょうか． 南海 じつはここに線型写像と行列式の内容が隠れている．ベクトル空間と 座標の関係は後に改めて考える． 例を，高校数学で習う 平面上のベクトルにとって，説明しよう．ベクトルの平行条件の問題です。ベクトルは平行移動して重なるものは同じものとみなすので、3点が同一直線上にある条件も同義です。 1． (1) 2つのベクトル$\vec{a}=\left( \begin

ベクトル

二つのベクトルの平行条件 南海 まずでない二つのベクトル とが平行である条件から考えよう． 史織 平行ということは方向が同じで大きさは違ってもよいということなので，0でない実数 で となるものがあることと同値です． とが平行，つまりなる があるとします．このとき なので， です． 逆にとします． ならなのでとなりとは平行，のときも同様． と反対向きに平行 ˇ ~a * ~b ¶ベクトルの平行条件 ‡ ~a 6=~0，~b 6=~0 のとき ~a==~b ~b = k~a となる実数kがある µ · 例15 j~aj = 2 とする．~aと平行で大きさが1のベクトルは 1 2 ~a と¡ 1 2 ~a 注意 1 2 ~aを ~a 2 と書くこともある． 大きさが1のベクトルを単位ベクトルという．・ベクトルの平行条件 公式 , 垂直 , ベクトル , 垂直条件 , ベクトルの垂直条件 , 『チャート式 数学ⅡB』 数研出版

空間ベクトルの平行条件 ， a → = (2 − 1 5) ， b → = (z – 1 2 z 1) のとき， a → ∥ b → となることはあるか．ベクトルaはもう一方のベクトルbのk倍ということで、a=kbと表す。」 といった認識で合っていますか？ もう一点、例えば、平行条件a=kbにk=1を代入して、 「ベクトルaとbが平行であるならば、k=1のとき、同じ大きさである。」 は分かるのですが、前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味している。 （証明） (h k l) 面上の以下の2本のベク をベクトルを考える。 a 1 − a 2 a 2 − a 3 h k, k l （310） この 2本ののクトルとベクトルと(29) の逆格子 ベクトル と

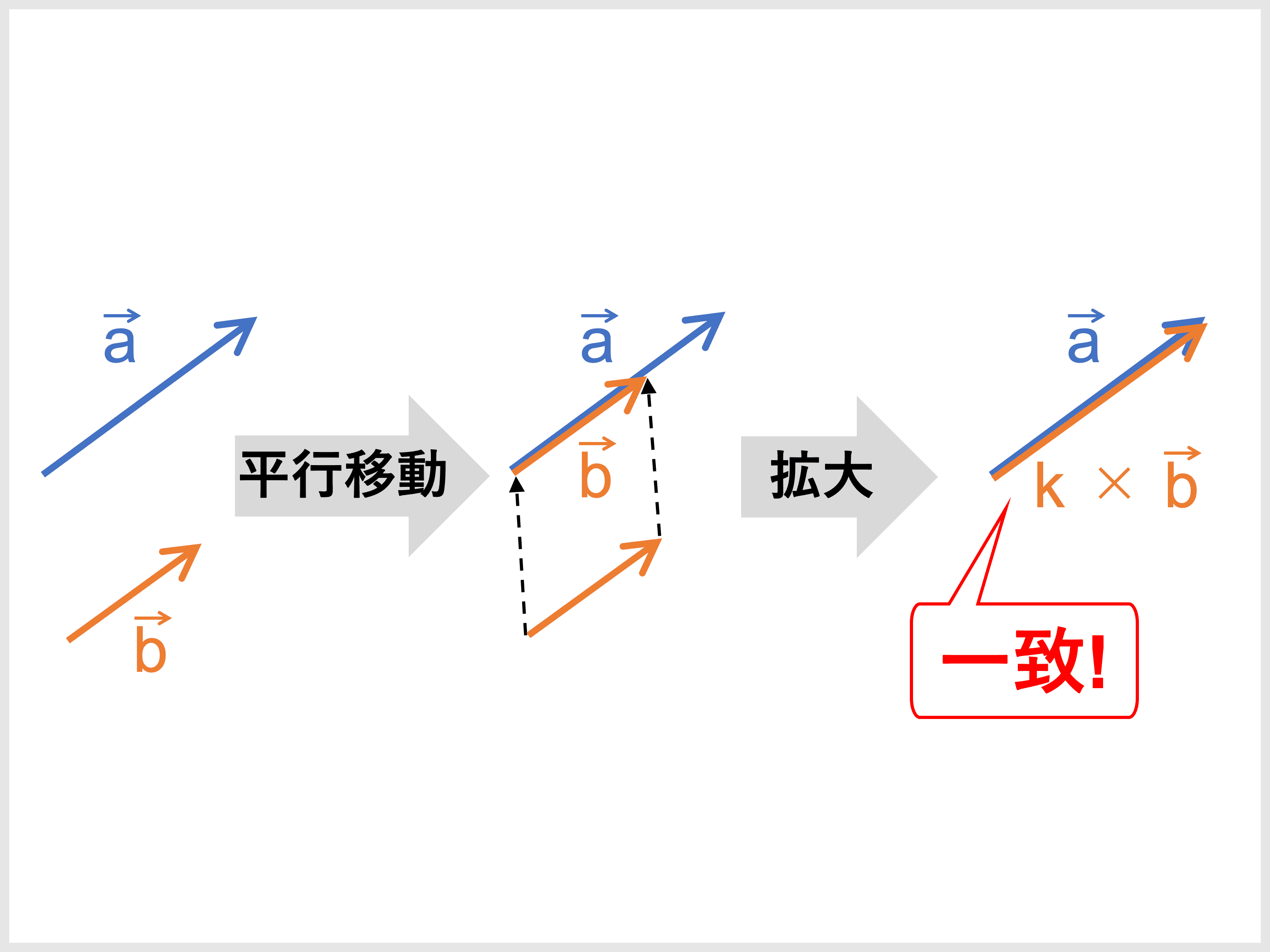
Apr 17,  · ベクトルの平行条件 \vec {0} でない 2 つのベクトル \vec {a} と \vec {b} が平行であるとき、 \vec {b} は 平行移動 によって \vec {a} が定める直線上に移すことができます。 そして、移動した \vec {b} は 適当な大きさに引き伸ばす ことで \vec {a} に一致させることができます。 だから、任意の実数 k を使って \vec {a} = k \vec {b} と表せるのですね。以下の条件を満たすとき，二本の平面ベクトル v undefined 1, v undefined 2 \overrightarrow{v}_1,\overrightarrow{v}_2 v 1 , v 2 は一次独立という。 条件： c 1 v undefined 1 c 2 v undefined 2 = 0 undefined c_1\overrightarrow{v}_1c_2\overrightarrow{v}_2=\overrightarrow{0} c 1 v 1 c 2 v 2 = 0 を満たす実数 c 1 , c 2 c_1,c_2 c 1 , c 2 の組が c 1 = c 2 = 0 c_1=c_2=0 c 1 = c 21 章05 ベクトルの平行条件 問題 ===== ↑ 1 学期中間テスト ↑ ===== 要点まとめ 考査前演習 gw課題 1 章06 ベクトルの内積1 問題 1 章07 ベクトルの内積2 / 垂直条件 問題

中３ ２直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

ベクトルの演算 ベクトルの加法と減法 Ppt Download

空間ベクトル(3 次元ベクトル) a,b (‰ 0) が平行でないとき, a,b の両方と直交し, a,b,n が右手系(下で説明す る) となるような大きさ1 のベクトルn が一意に定まる このとき, a,b のなす角をθ (0 ő θ ő π) として, a とb の外積aˆb をLongitudinal wave ）：振動が波の進行方向（波数ベクトル）に対して平行 横波（ Transverse wave）：振動が波の進行方向（波数ベクトル）に対して垂直 但し、電磁波（光波）は横波なので、以下では、横波のみ扱う 横波の条件 (,, 0 tt) ( ) x y z xy z ∂ψ ∂ψ ∂ψFeb 06, 19 · ベクトルの平行条件 \( \vec{ a } \neq \vec{ 0 } \)，\( \vec{ b } \neq \vec{ 0 } \) のとき \( \vec{ a } \ /\!/ \ \vec{ b } \ \Longleftrightarrow \ \vec{ b } = k \vec{ a } \) となる実数 \( k \) がある

高校数学b ベクトルの内積とax Byの最大最小 受験の月

ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典

に平行な直線となる。 なら条件を満たすこと したがって、 与えられたベクトルが一次従属であることと、 上記方程式の一般解が1以上の自由度（パラメータの数）を持つ、という条件も同値。今回のテーマは ベクトルの平行条件と成分 です。 2つのベクトルが平行であるための条件 について学習していきましょう。 「ベクトルbがベクトルaの実数倍」ならば平行Jun 15, 19 · 平行条件には前提条件\ a0,\ b0があるので,\ 解答ではこれを確認した上で適用している y成分が0ではないので,\ ab0,2ab0である スポンサーリンク 高校数学B 平面ベクトルと平面図形

考え方はわかります 方向ベクトルがどうして 1 0 0 に 高校数学に関する質問 勉強質問サイト

ベクトルの平行条件 垂直条件

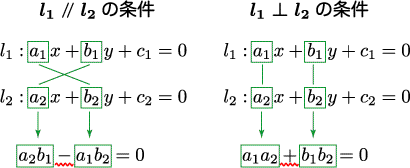
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。（定義） 2 2組の向かいあう辺が、それぞれ等しい。（証明） 3 2組の向かいあう角が、それぞれ等しい。（証明）ベクトルの平行条件については、以前にも学習しましたね。 あるベクトルCDが、別のベクトルABの実数k倍である とき、 AB//CD が成り立ちました。 その逆も真であり、 「ベクトルCDがベクトルABの実数倍」⇔「ベクトルABとベクトルCDは平行」 が成り立ちます。２直線の平行条件 複素数平面上に４点 A (z 1), B (z 2), C (z 3), D (z 4) があるとき， AB//CD となるための条件は z 4 −z 3 =k (z 2 −z 1)

ベクトルの外積と平行四辺形の面積 身勝手な主張

ベクトルの基本公式 これで制覇 Okenavi

May 22,  · ベクトルは、高校数学の中でも苦手な人が多い分野ですよね。そこでこの記事では、ベクトルを解く上で非常に重要な内積の求め方を、ベクトルの垂直・平行条件と併せてご紹介します。この記事を読んでベクトルの内積を使いこなしましょう！2直線の平行条件と垂直条件（基本形） これはこの2直線の法線ベクトル $(a,b)$ と $(a',b')$ の内積が $0$ 、すなわち垂直なベクトルであることを示している。空間ベクトルの平行条件あるいは3点が同一直線上にある条件 (共線条件)の問題です。 1．((1) 立教大 (2) 北里大) (1) 3点A$(2,3,4)$, B$(3,2,1)$, C$(m,

直線の方程式ax By C 0型の意味と垂直条件 平行条件 ラディカル高校数学

高校数学b ベクトルの垂直条件 映像授業のtry It トライイット

Oct 27, 15 · 「平行」と同じ条件になりますので、確認しておいて下さい。 だから平行になる条件としては、 \( 実数 \color{red}{k} を用いて \vec{a}3 \vec{b}=\color{red}{ k}( \vec{b} \vec{a})\)二つの零ベクトルでない平面ベクトル ~ a, ~ b が平行であるための条件は ~ a × ~ b = 0 となることである． 外積の符号 平面ベクトルの外積の絶対値は平行四辺形の面積としての意 味をもつが，さらに，その符号について考えよう． 図 12 ~a と ~ b の位置関係< ベクトルの平行条件> 零ベクトルでない2つのベクトルaとbが平行(a // b)であるということは互いに 他の定数倍(a = kbまたはb = kaとなる定数k が存在する)ということである。 これが成立するための条件を平面と空間の場合にそれぞれ示す。 1

2 がわかりません 答え見てもわからないのですか やり方はこれしかないですか Clear

高2 数学b 2章 1節 平面上のベクトル 高校生 数学のノート Clear

ベクトルと中点連結定理 中学のときに習う中点連結定理を、ベクトルの世界で考えてみましょう。 三角形 ABC があって、辺 AB, AC の中点を、それぞれ M, N とおきます。 このとき、 MN は BC と平行で、長さが $\dfrac{1}{2}$ になる、というのが、中点連結定理の内容です。④ 逆ベクトルの性質 a(−a)=0,(−a)a = 0 G12 ベクトルの平行条件 a 6= 0, b 6= 0のとき a // b ⇐⇒ a = kb またはb = la の形に表される。 G13 ベクトルと実数の積の基本法則 ベクトルa, bと実数k, l に対して， ① 結合法則 (kl)a = k(la) ② 分配法則 (k l)a = kala2以下の条件を満たすように、 の値を定めなさい。 ベクトル d ， ，e ， に対し、d e と d e が平行 ベクトル d ， ，e ， に対し、d e と e d が平行 3四角形 $%&' が平行四辺形になるためには、$' %&

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

ベクトル 同一平面上の条件 時習館 ゼミナール 高等部

ベクトルの平行条件の教科書例題が意味が分かりません。 以下ベクトル 「a=2とする。aと平行で大きさが1のベクトルは？」 大きさ1とはなんのことですか？k？b？ それにa=2って分 かっているのにベクトルの成分表示を用いて計算できない。 評価項目3 ベクトルの内積を求めて，応用できる。 ベクトルの内積を求めることができる。 ベクトルの内積を求めることができない。 評価項目4 ベクトルの平行・垂直条件を利用して，応用できる。ベクトルの平行条件 ， a → = (− 2 3) ， b → = (4 x) のとき， a → と b → が平行であるように x の値を定めよ．

３点が一直線上にある時のベクトルが満たす条件 塾を探す前に読むブログ

高校 数学b ベクトル１０ 平行条件 １３分 Youtube

ベクトルの平行条件です。 平行の時は a ベクトル=k b ベクトル ですよね？

ベクトルの解析幾何学への応用２ ２直線の垂直条件 平行条件 身勝手な主張

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

高校数学b 平行六面体と空間ベクトルの演算 受験の月

てらtube 数ｂ ベクトル 6 ベクトルの平行条件 Youtube

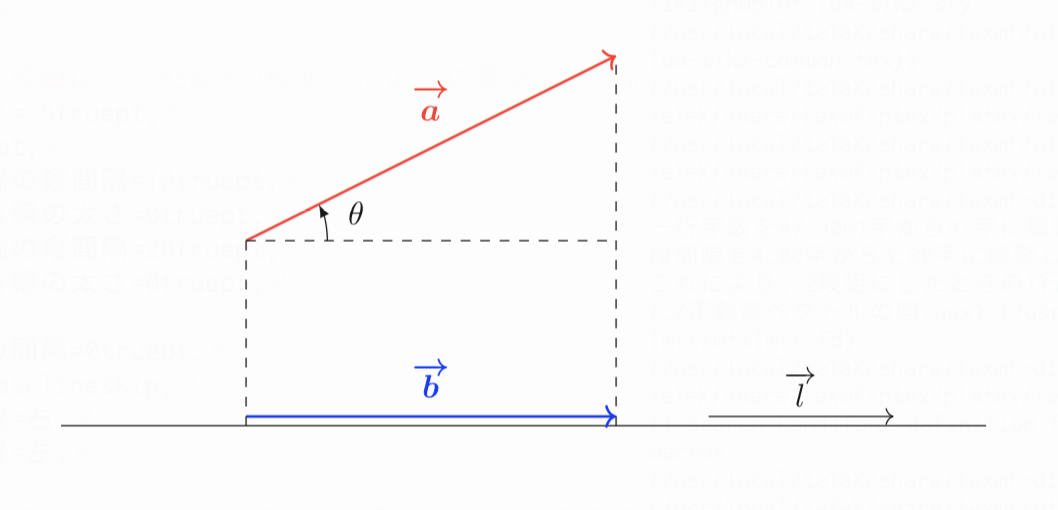
正射影ベクトルの公式は 平面や空間での入試問題を東大医学部生が解説 東大医学部生の相談室

２直線の平行と垂直条件 思考力を鍛える数学

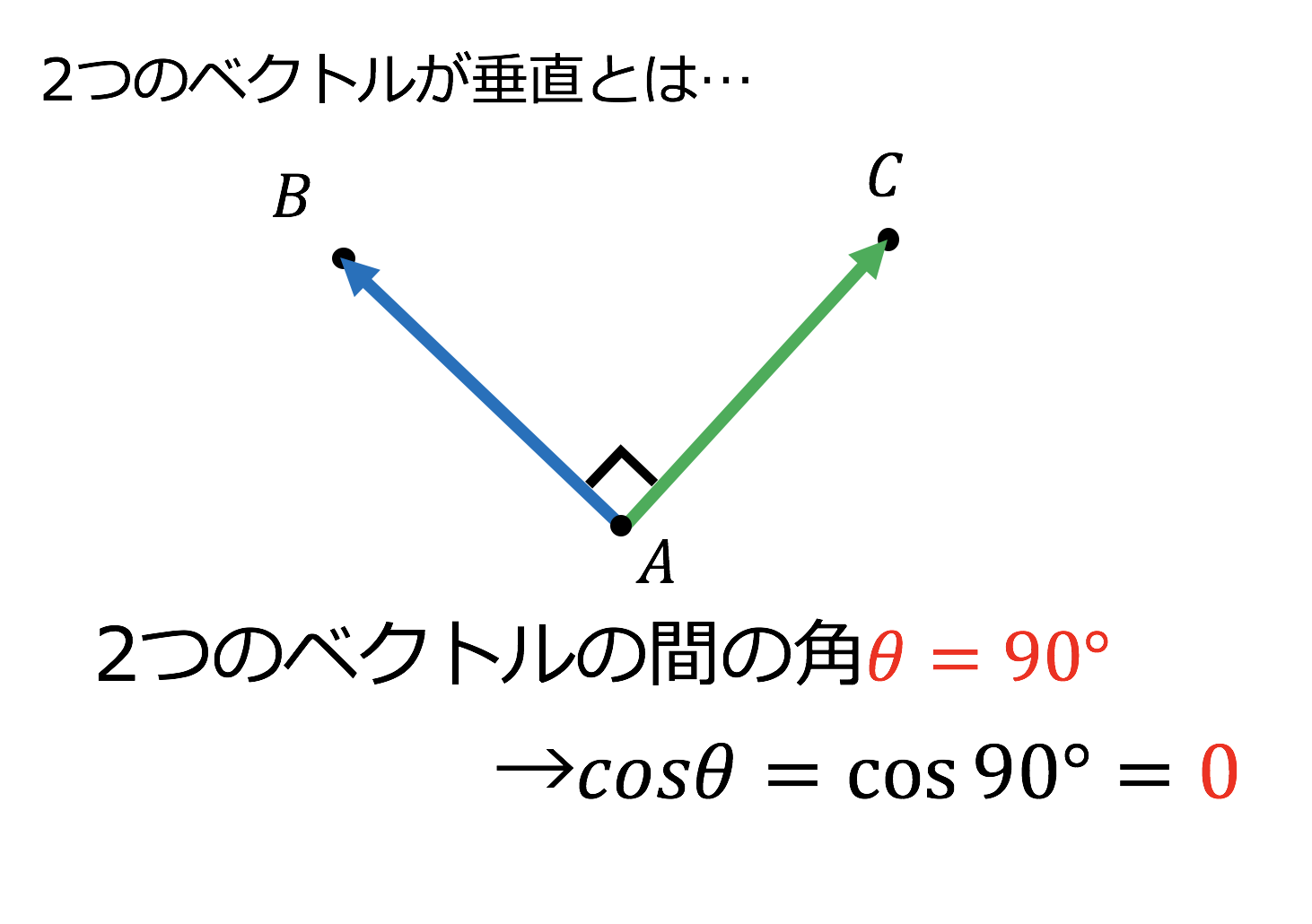
3分で分かる ベクトルの内積の2つの求め方 垂直 平行条件についてわかりやすく 合格サプリ

複素数平面 高校数学に関する質問 勉強質問サイト

2つの直線が平行 垂直となる条件 数学の偏差値を上げて合格を目指す

高校数学b ベクトルの平行条件 映像授業のtry It トライイット

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学b ベクトルの平行条件 映像授業のtry It トライイット

高校数学 ベクトル 第6講 問3 ベクトルの平行条件の利用 標準レベル Youtube

並行になる条件ですがたとえbaベクトル Cdベクトルのように向かい合った辺が同じ向き Clear

Vecavecb1 Vecc1dfracsqrt3 Lihat Cara Penyelesaian Di Qanda

ベクトルの垂直条件 平行条件を教えてください 三次元だとして 二つのベ Yahoo 知恵袋

ベクトルの平行条件 垂直条件

高校数学b 直線のベクトル方程式 １ 映像授業のtry It トライイット

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

高校数学 ベクトル 第3講 内積の成分表示 平行条件 垂直条件 標準レベル Youtube

スローライフの森 数１ 自家菜園 大人のさび落とし 009 ベクトルと図形

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

中３ ２直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

数学ii Bチェック リピート 第8章 1和と実数倍 3 平行条件 Pukiwiki

数学二つのベクトルが平行になる条件はa Kbじゃないんですか 写真の問題の解説 Yahoo 知恵袋

下の問題なのですが 単位ベクトルの考え方が分からず 自分なり 高校数学に関する質問 勉強質問サイト

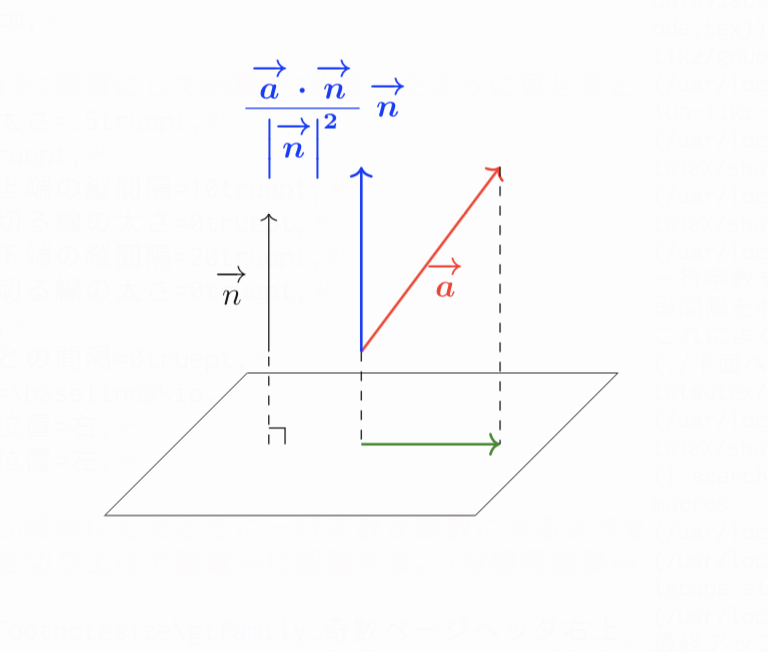
正射影ベクトルの公式は 平面や空間での入試問題を東大医学部生が解説 東大医学部生の相談室

空間ベクトルの成分表示と垂直 平行条件をわかりやすく

数学bのベクトルの平行条件の問題なんですけど 合っていますか 間違えて Yahoo 知恵袋

空間ベクトル 直線と平面の交点の位置ベクトルの求め方 数学b 定期テスト対策サイト

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

個別指導アプリ スナップアスク 本日の問題 今回はベクトルの平行条件です この公式 暗記で済ませていませんよね 高校数学 数学b 受験生 受験勉強 ベクトル

ベクトルの平行条件の問題です 問9の答えを教えてほしいです なるべく早くお願 Yahoo 知恵袋

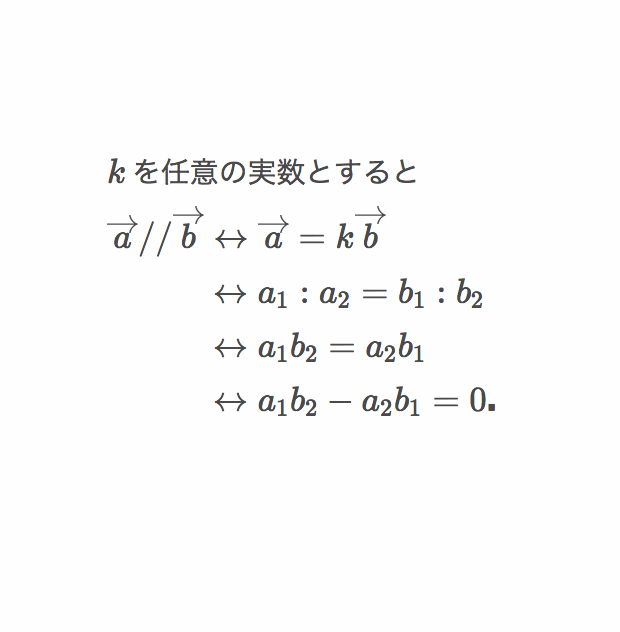
個別指導アプリ スナップアスク 本日の問題 今回はベクトルの平行条件です この公式 暗記で済ませていませんよね 高校数学 数学b 受験生 受験勉強 ベクトル

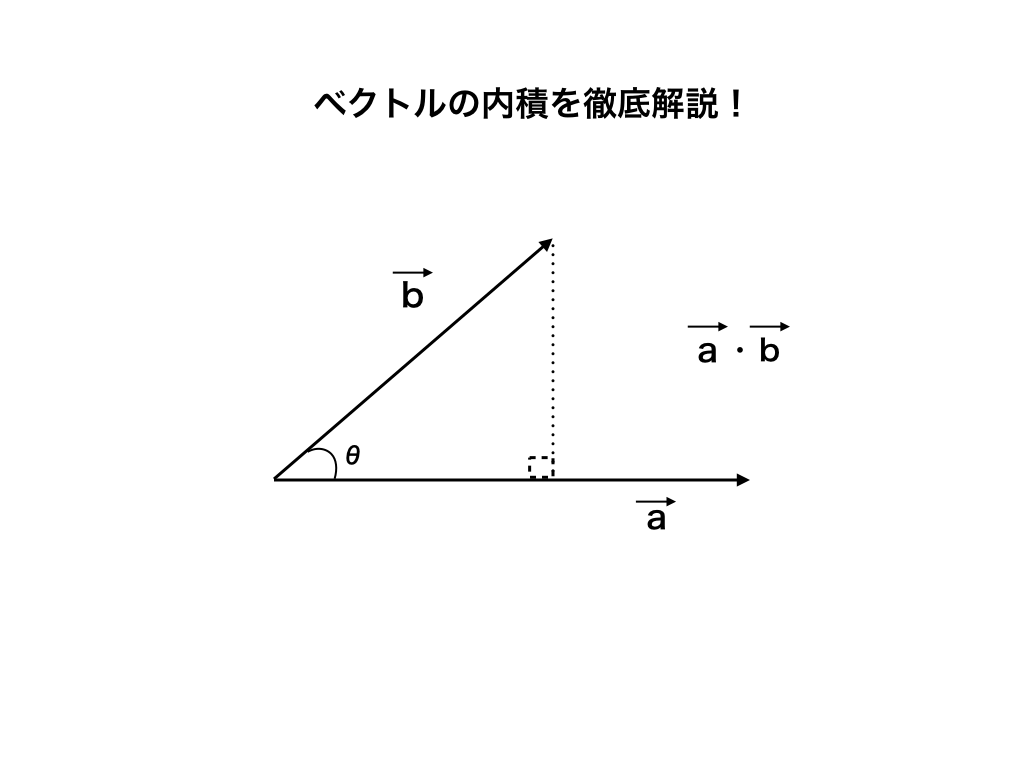
内積とは 定義と求め方 公式を解説 ベクトルの掛け算を分かりやすく

ベクトルの平行条件 高校数学に関する質問 勉強質問サイト

Studydoctor平行な直線のベクトル方程式と媒介変数 数ｂ Studydoctor

ベクトル

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

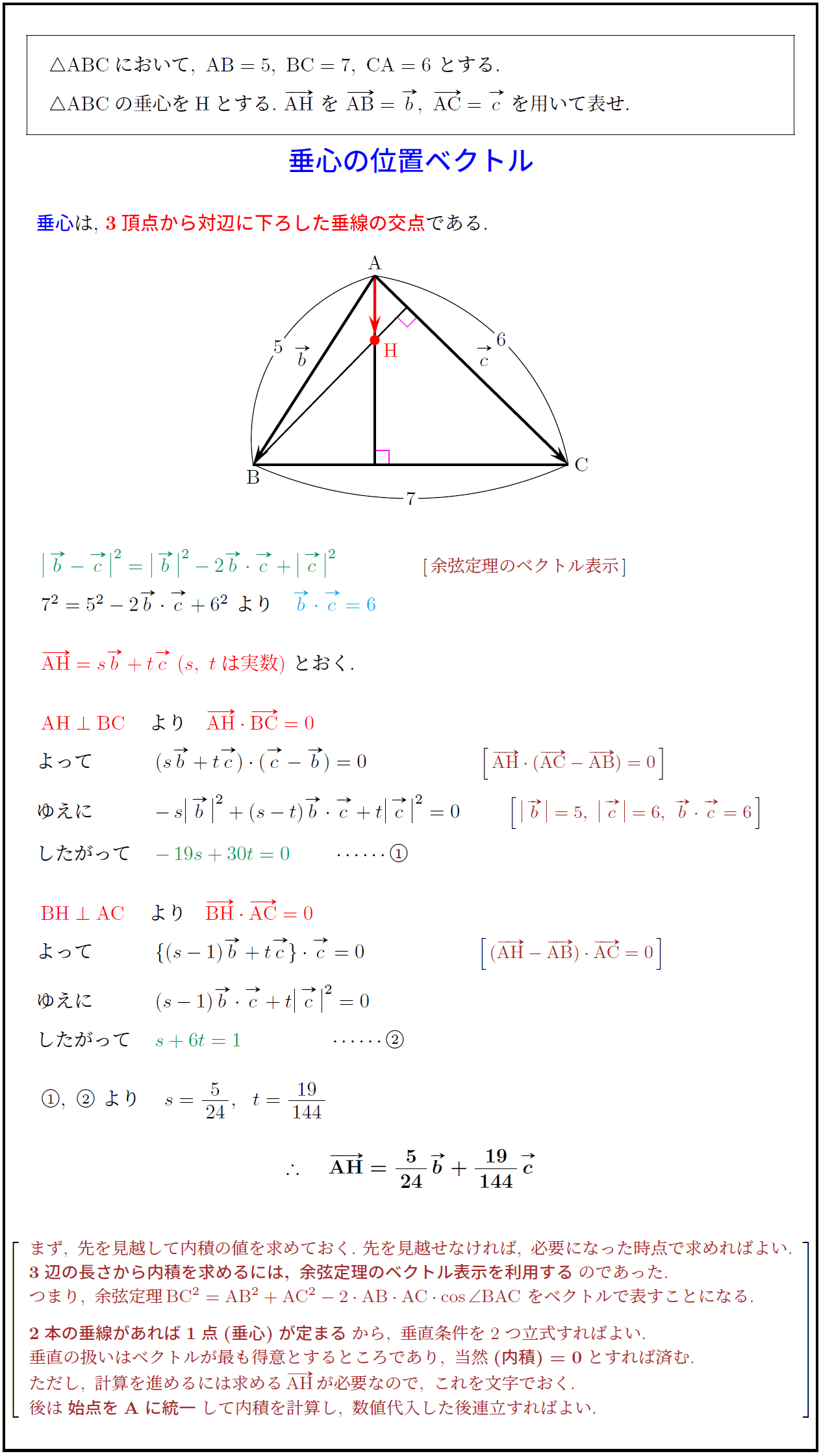
高校数学b 三角形の垂心の位置ベクトル 受験の月

直線の方程式ax By C 0型の意味と垂直条件 平行条件 ラディカル高校数学

高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月

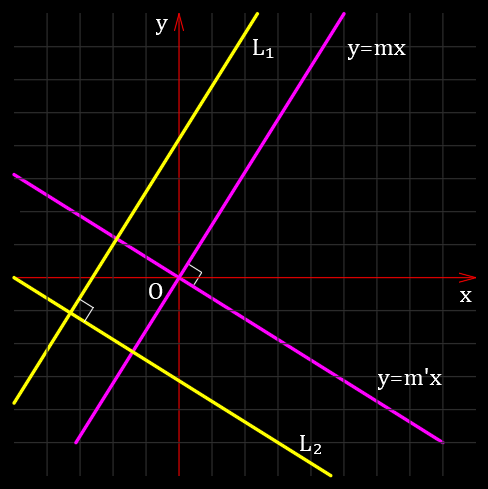
平行な直線と垂直な直線 Qiita

ベクトルの平行条件は理解しているが このタイプの問題は解き 高校数学に関する質問 勉強質問サイト

ベクトルでは 恒等式のような考え方はできないのでしょうか 高校数学に関する質問 勉強質問サイト

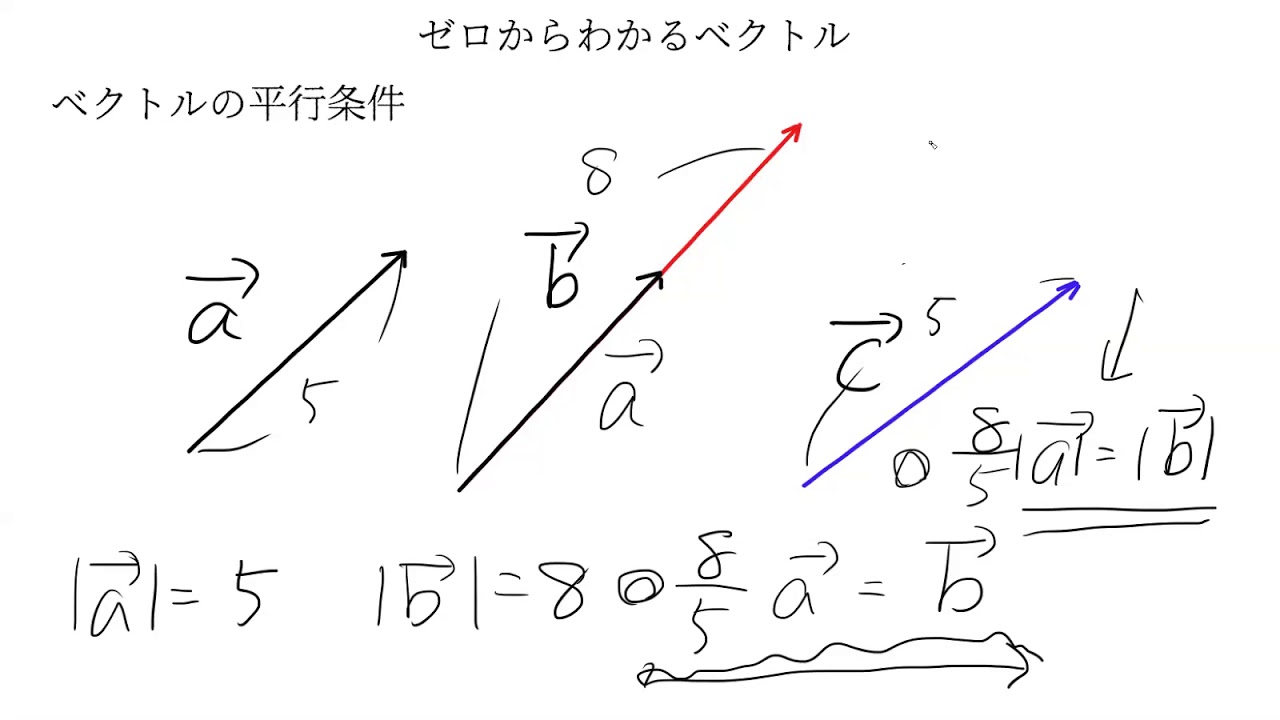
ベクトルの平行条件 ゼロからわかるベクトル第５回 Youtube

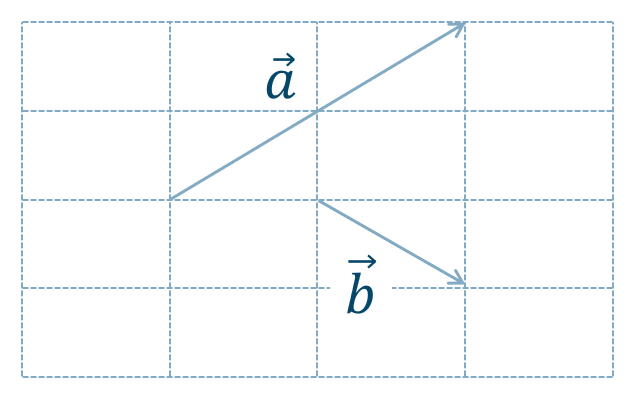
教科書レベルの問題一覧と解答 数学ｂ 平面ベクトル 教科書より詳しい高校数学

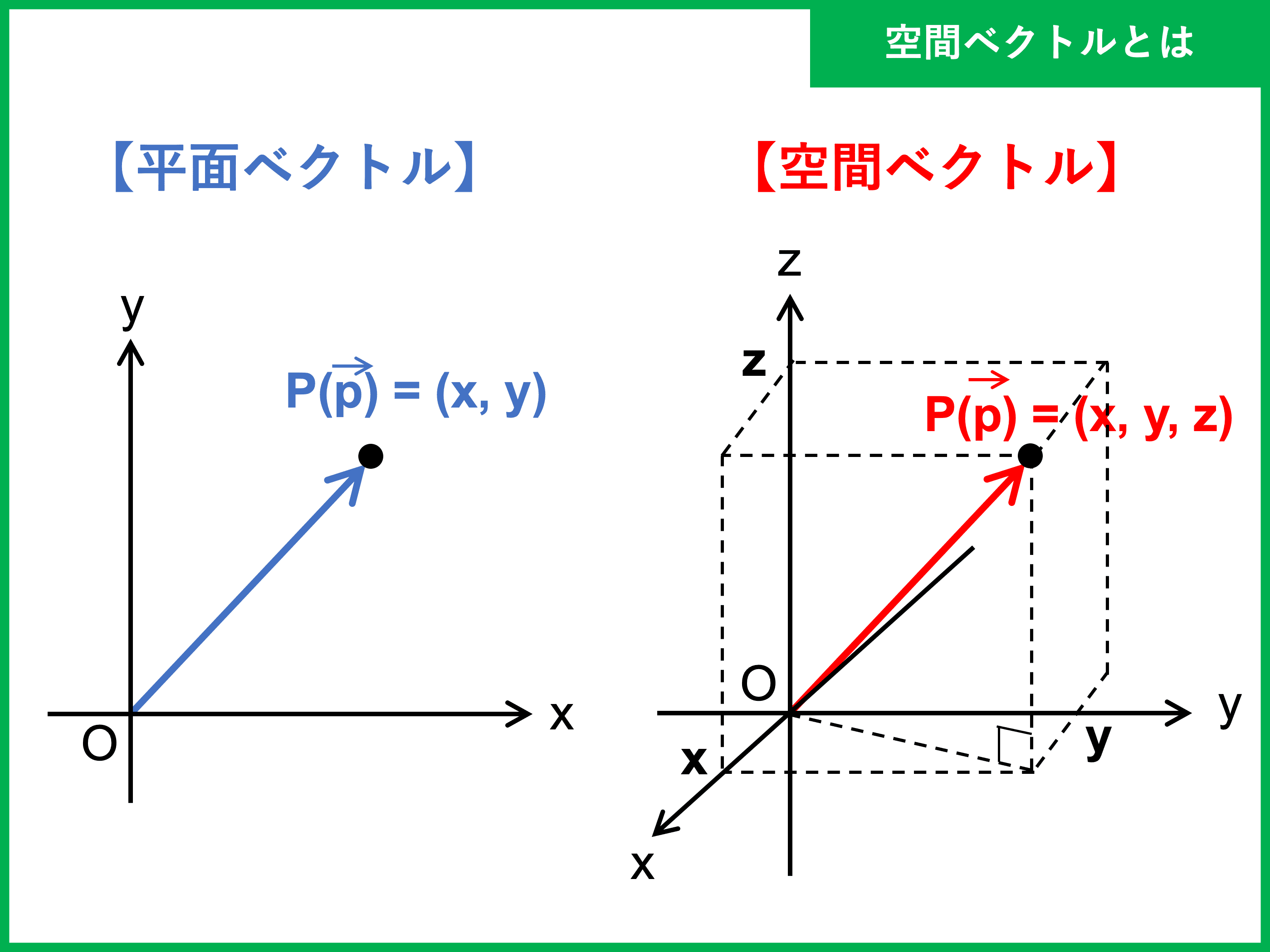
空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典

高校数学b 共面条件 4点が同一平面上にある条件 空間ベクトル最重要事項 受験の月

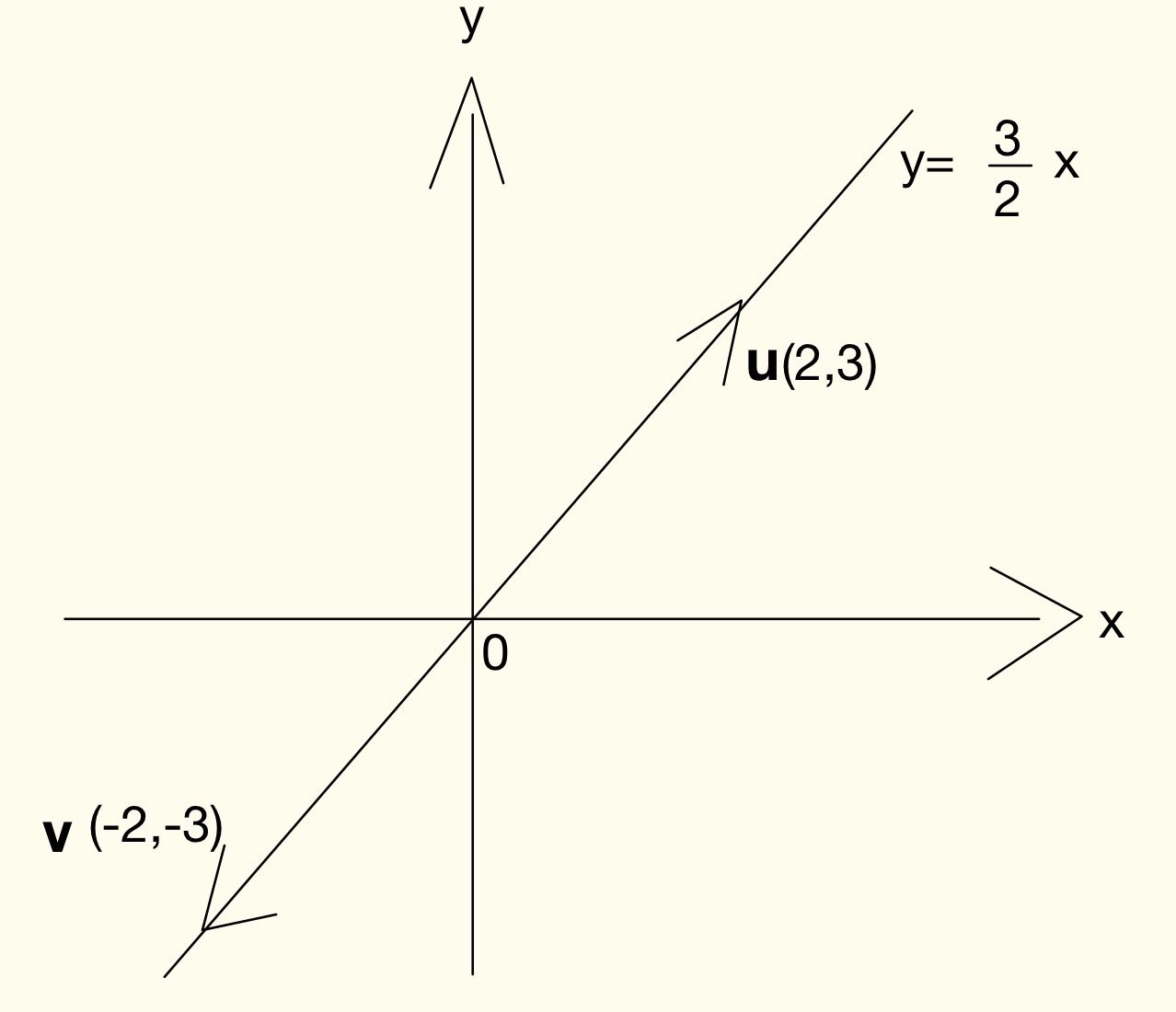
2つのベクトルの平行条件と直角条件 受験初心者へ

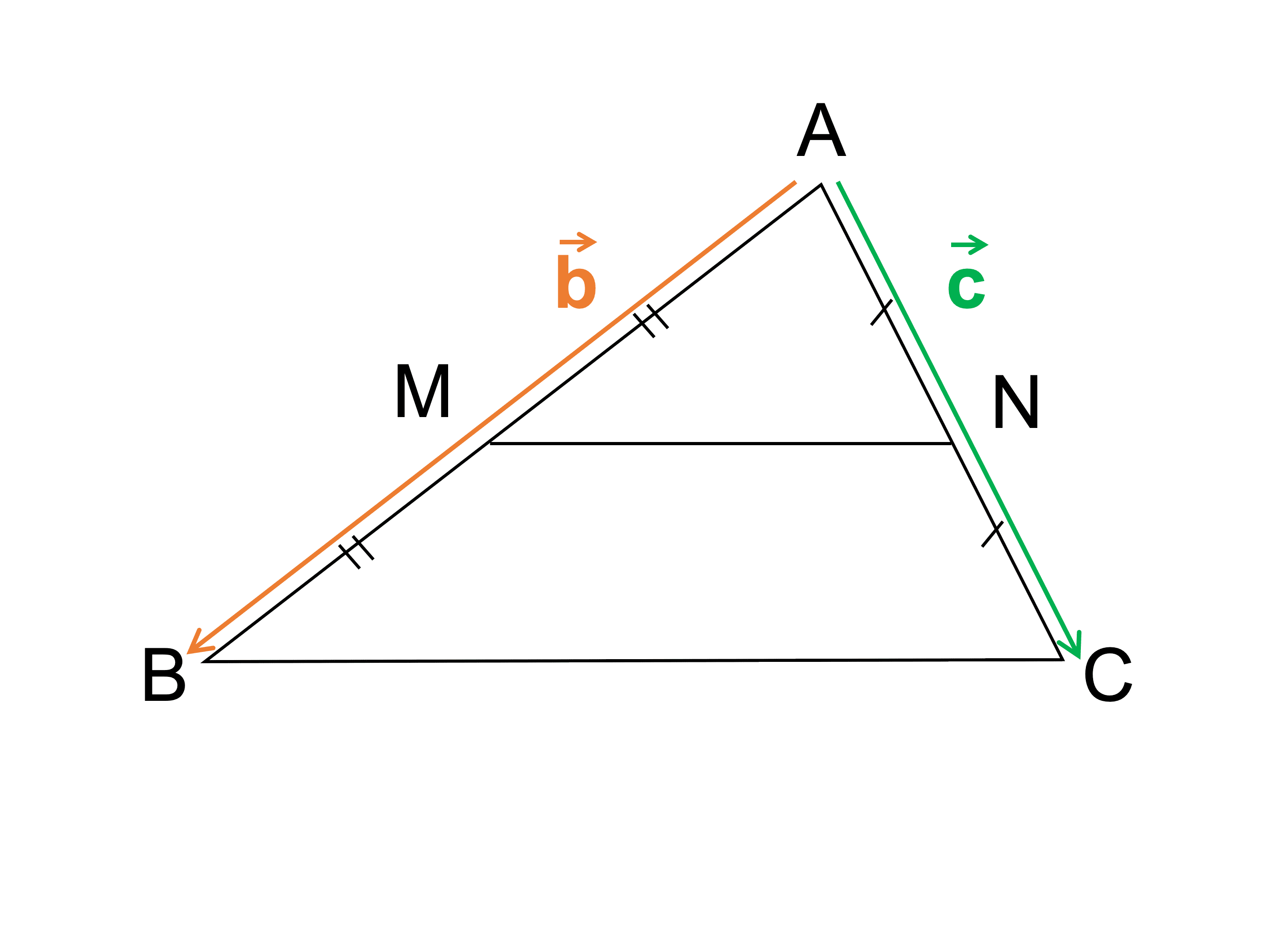
ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典

Studydoctor空間ベクトルの成分と平行 数ｂ Studydoctor

勉強しよう数学 空間ベクトルの３つの公式

高校数学b ベクトルの共点条件 複数の点が一致する条件 受験の月

多様体上の接続と平行移動 初級mathマニアの寝言

数学b編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス

ベクトルの平行条件 数学b フリー教材開発コミュニティ Ftext

ベクトル方程式の問題です 高校数学に関する質問 勉強質問サイト

高校数学b ベクトルの成分 映像授業のtry It トライイット

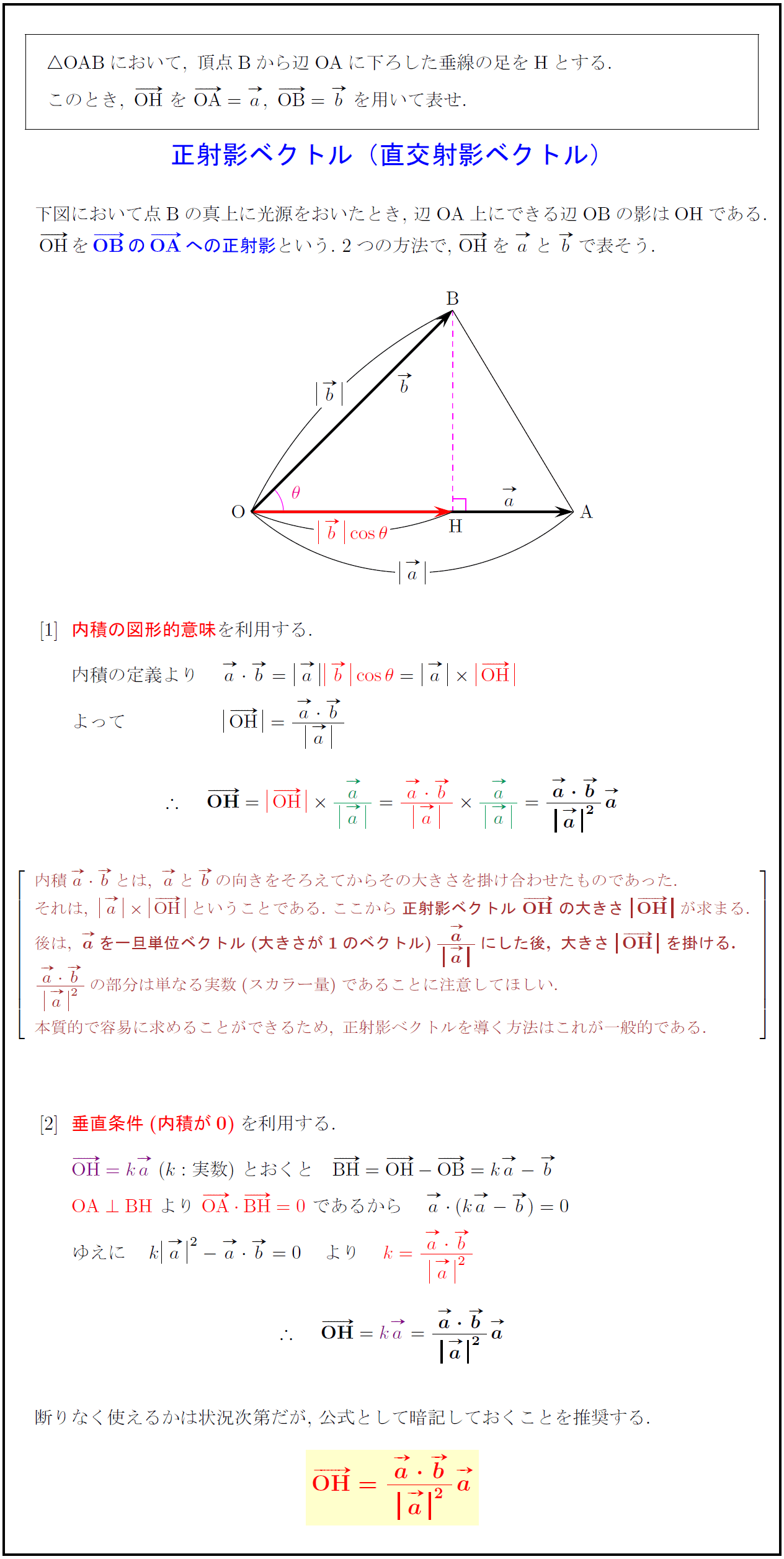
高校数学b 正射影ベクトル 直交射影ベクトル 受験の月

平行と垂直 ３ 怜悧玲瓏 高校数学を天空から俯瞰する

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する

ベクトル方程式を超わかりやすく解説した 理系ラボ

空間ベクトルの成分表示と垂直 平行条件をわかりやすく

平面ベクトル 平行条件 オンライン無料塾 ターンナップ Youtube

ベクトルの解析幾何学への応用１ 円の接線の方程式 身勝手な主張

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

数学ｂ ベクトルの成分と平行条件の使い方とコツ 教科書より詳しい高校数学

高校数学b ベクトルの共線条件 3点が一直線上にある条件 受験の月

平面ベクトルの平行条件についてです 画像の2 の2の最後の Yahoo 知恵袋

数学ii 平行条件と垂直条件 高校数学に関する質問 勉強質問サイト

基本 空間ベクトルの成分と平行 数ｂ空間ベクトル2 09 Youtube

ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典

数学b 平面ベクトル 6 1 共線条件 Youtube

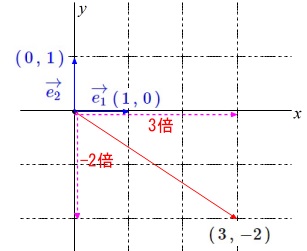
平面ベクトルの要点

高校数学b ベクトルの平行条件 映像授業のtry It トライイット

回答の初めにある条件でapベクトル 0がなぜあるのかが分かりません Clear

高校数学b ベクトルの成分 練習編 映像授業のtry It トライイット

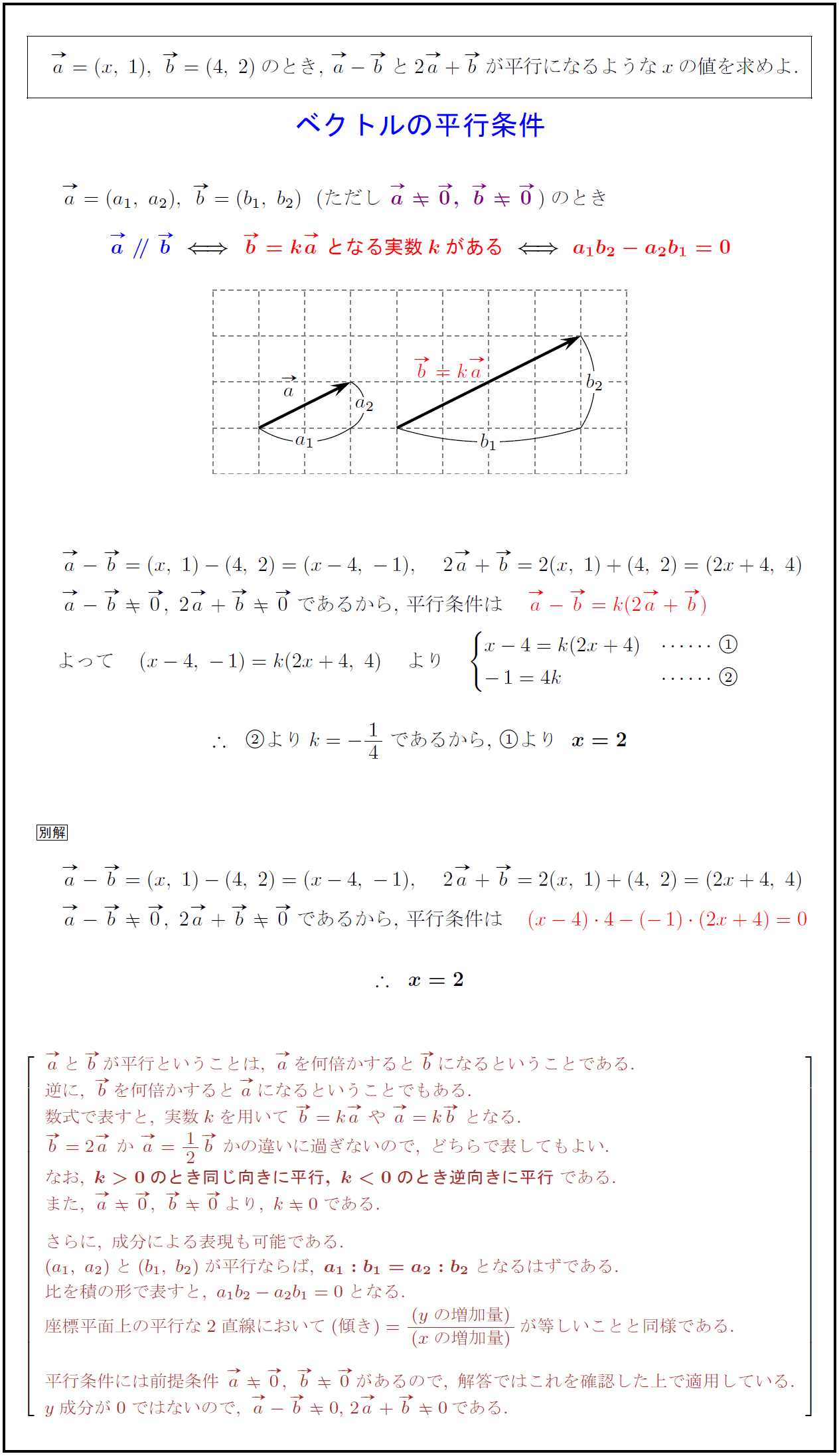
高校数学b ベクトルの成分表示と平行条件 受験の月

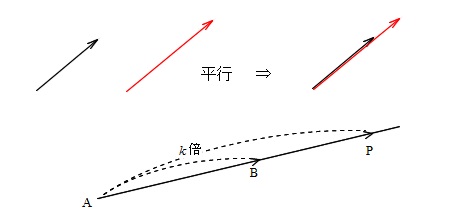
ベクトルの基本 平行と３点が一直線上にある条件

高校数学b ベクトルの成分表示と平行四辺形 受験の月

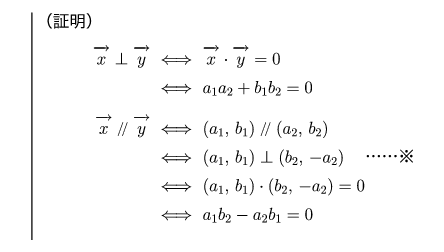
中３ ２直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

Incoming Term: ベクトル 平行 条件, ベクトル 平行 条件 証明,